Newton's Method and Fisher Scoring (KL Chapter 14)

Consider maximizing log-likelihood function $L(\mathbf{\theta})$, $\theta \in \Theta \subset \mathbb{R}^p$.

1  Notations

• Gradient (or score) of $L$: $$\nabla L(\theta) = \begin{pmatrix} \frac{\partial L(\theta)}{\partial \theta_1} \\ \vdots \\ \frac{\partial L(\theta)}{\partial \theta_p} \end{pmatrix}$$

• Hessian of $L$:
  $$\nabla^2 L(\theta) = \begin{pmatrix} \frac{\partial^2 L(\theta)}{\partial \theta_1 \partial \theta_1} & \dots & \frac{\partial^2 L(\theta)}{\partial \theta_1 \partial \theta_p} \\ \vdots & \ddots & \vdots \\ \frac{\partial^2 L(\theta)}{\partial \theta_p \partial \theta_1} & \dots & \frac{\partial^2 L(\theta)}{\partial \theta_p \partial \theta_p} \end{pmatrix}$$

• Observed information matrix (negative Hessian):

$$- \nabla^2 L(\theta)$$

• Expected (Fisher) information matrix: $$\mathbf{E}[- \nabla^2 L(\theta)].$$

2  Newton's method

• Newton's method was originally developed for finding roots of nonlinear equations $f(\mathbf{x}) = \mathbf{0}$ (KL 5.4).

• Newton's method, aka Newton-Raphson method, is considered the gold standard for its fast (quadratic) convergence $$\frac{\|\mathbf{\theta}^{(t+1)} - \mathbf{\theta}^*\|}{\|\mathbf{\theta}^{(t)} - \mathbf{\theta}^*\|^2} \to \text{constant}.$$

• Idea: iterative quadratic approximation.

• Taylor expansion around the current iterate $\mathbf{\theta}^{(t)}$ $$L(\mathbf{\theta}) \approx L(\mathbf{\theta}^{(t)}) + \nabla L(\mathbf{\theta}^{(t)})^T (\mathbf{\theta} - \mathbf{\theta}^{(t)}) + \frac 12 (\mathbf{\theta} - \mathbf{\theta}^{(t)})^T [\nabla^2L(\mathbf{\theta}^{(t)})] (\mathbf{\theta} - \mathbf{\theta}^{(t)})$$ and then maximize the quadratic approximation.

• To maximize the quadratic function, we equate its gradient to zero $$\nabla L(\theta^{(t)}) + [\nabla^2L(\theta^{(t)})] (\theta - \theta^{(t)}) = \mathbf{0}_p,$$ which suggests the next iterate $$\begin{eqnarray*} \theta^{(t+1)} &=& \theta^{(t)} - [\nabla^2L(\theta^{(t)})]^{-1} \nabla L(\theta^{(t)}) \\ &=& \theta^{(t)} + [-\nabla^2L(\theta^{(t)})]^{-1} \nabla L(\theta^{(t)}). \end{eqnarray*}$$ We call this naive Newton's method.

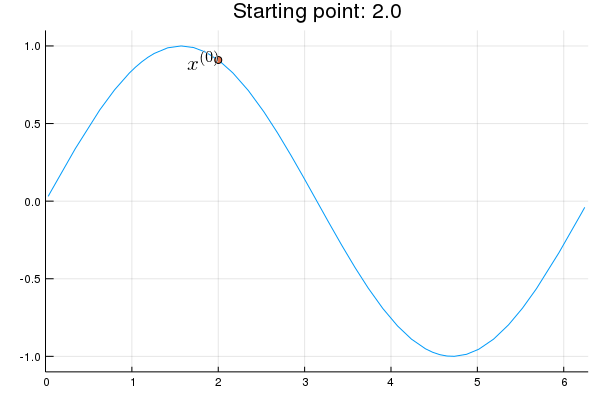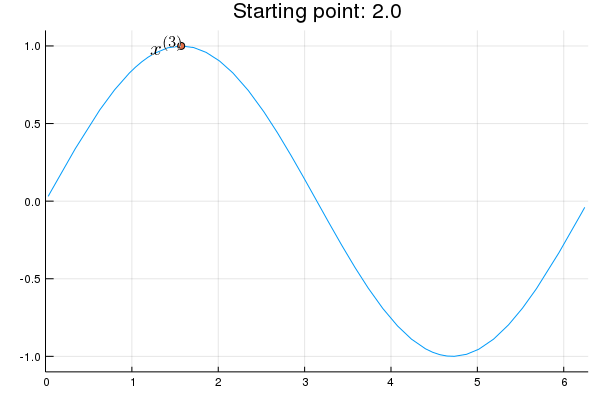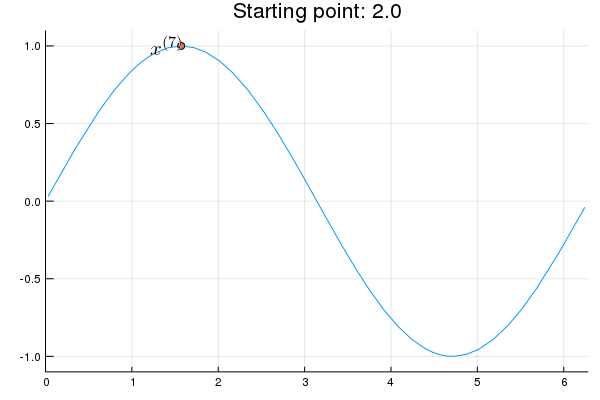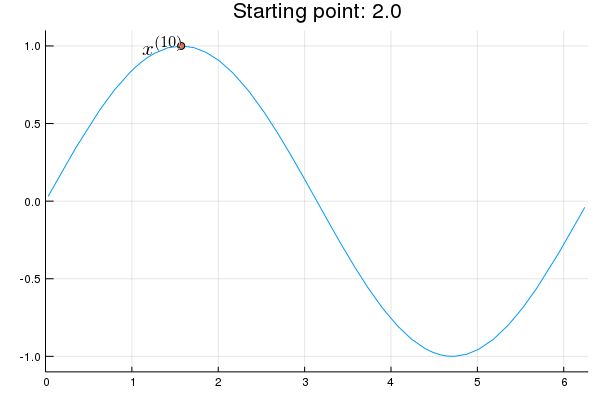
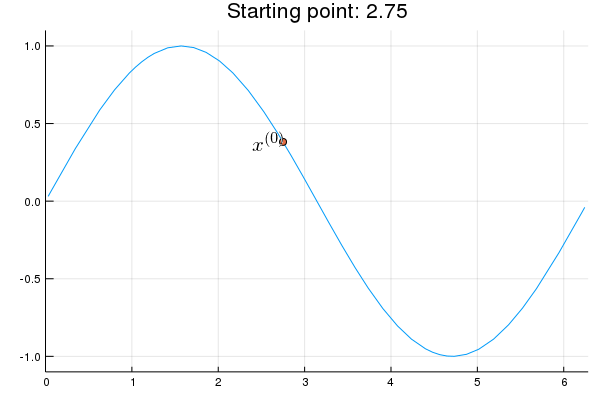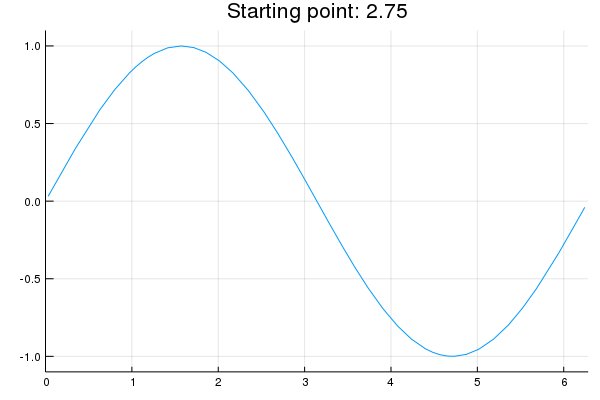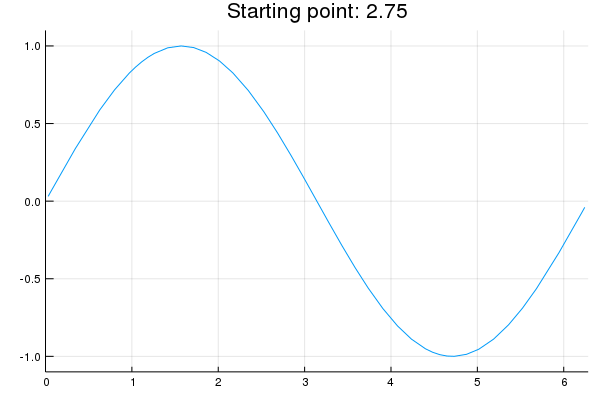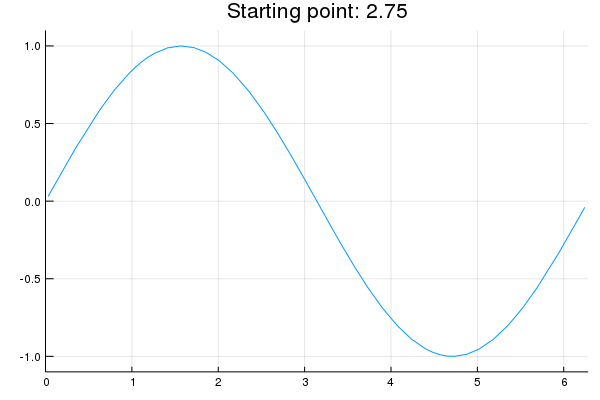
• Stability issue: naive Newton's iterate is not guaranteed to be an ascent algorithm. It's equally happy to head uphill or downhill. Following example shows that the Newton iterate converges to a local maximum, converges to a local minimum, or diverges depending on starting points.

using Plots; gr()
using LaTeXStrings, ForwardDiff

f(x) = sin(x)
df = x -> ForwardDiff.derivative(f, x) # gradient
d2f = x -> ForwardDiff.derivative(df, x) # hessian
x = 2.0 # start point: 2.0 (local maximum), 2.75 (diverge), 4.0 (local minimum)
titletext = "Starting point: $x"
anim = @animate for iter in 0:10
    iter > 0 && (global x = x - d2f(x) \ df(x))
    p = Plots.plot(f, 0, 2π, xlim=(0, 2π), ylim=(-1.1, 1.1), legend=nothing, title=titletext)
    Plots.plot!(p, [x], [f(x)], shape=:circle)
    Plots.annotate!(p, x, f(x), text(latexstring("x^{($iter)}"), :right))
end
gif(anim, "./tmp.gif", fps = 1);

┌ Info: Saved animation to 
│   fn = /Users/huazhou/Documents/github.com/ucla-biostat-257-2021spring.github.io/slides/23-newton/tmp.gif
└ @ Plots /Users/huazhou/.julia/packages/Plots/YicDu/src/animation.jl:104

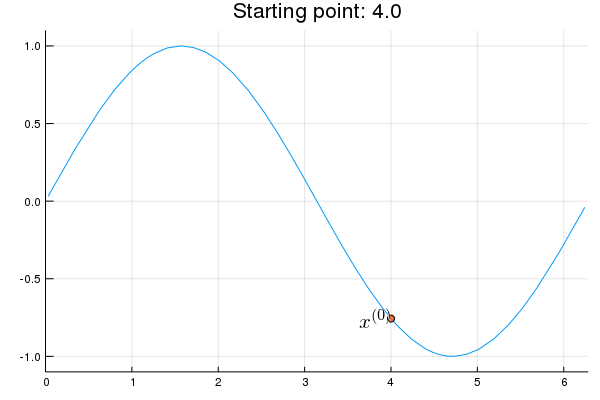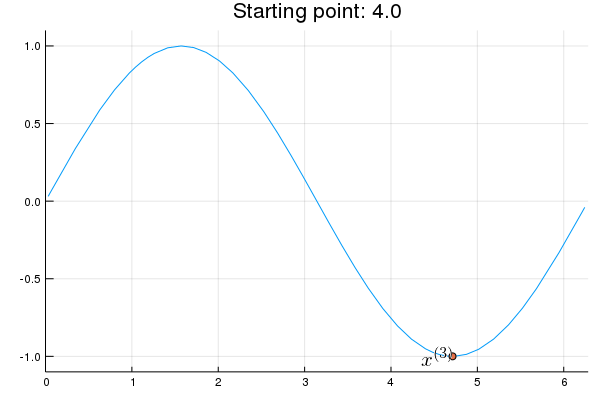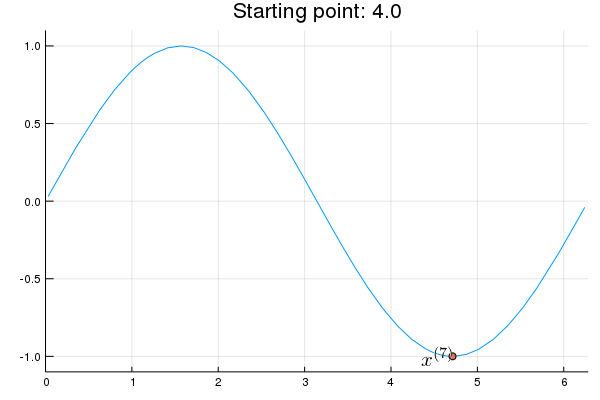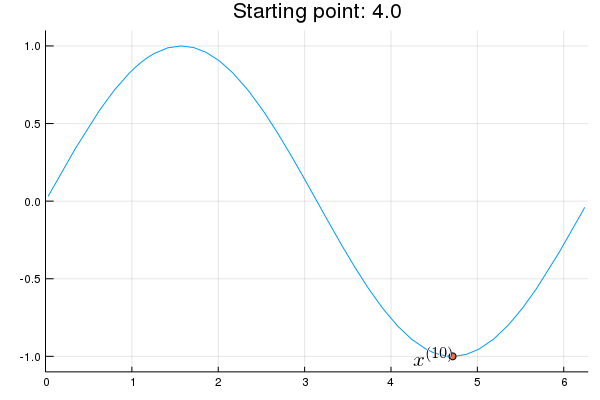
• Remedies for the instability issue:

  1. approximate $-\nabla^2L(\theta^{(t)})$ by a positive definite $\mathbf{A}$ (if it's not), and
  2. line search (backtracking).

• Why insist on a positive definite approximation of Hessian? By first-order Taylor expansion, $$\begin{eqnarray*} & & L(\theta^{(t)} + s \Delta \theta^{(t)}) - L(\theta^{(t)}) \\ &=& L(\theta^{(t)}) + s \cdot \nabla L(\theta^{(t)})^T \Delta \theta^{(t)} + o(s) - L(\theta^{(t)}) \\ &=& s \cdot \nabla L(\theta^{(t)})^T \Delta \theta^{(t)} + o(s) \\ &=& s \cdot \nabla L(\theta^{(t)})^T [\mathbf{A}^{(t)}]^{-1} \nabla L(\theta^{(t)}) + o(s). \end{eqnarray*}$$ For $s$ sufficiently small, right hand side is strictly positive when $\mathbf{A}^{(t)}$ is positive definite. The quantity $\{\nabla L(\theta^{(t)})^T [\mathbf{A}^{(t)}]^{-1} \nabla L(\theta^{(t)})\}^{1/2}$ is termed the Newton decrement.

• In summary, a practical Newton-type algorithm iterates according to $$\boxed{ \theta^{(t+1)} = \theta^{(t)} + s [\mathbf{A}^{(t)}]^{-1} \nabla L(\theta^{(t)}) = \theta^{(t)} + s \Delta \theta^{(t)} }$$ where $\mathbf{A}^{(t)}$ is a pd approximation of $-\nabla^2L(\theta^{(t)})$ and $s$ is a step length.

• For strictly concave $L$, $-\nabla^2L(\theta^{(t)})$ is always positive definite. Line search is still needed to guarantee convergence.

• Line search strategy: step-halving ($s=1,1/2,\ldots$), golden section search, cubic interpolation, Amijo rule, ... Note the Newton direction
  $$\Delta \theta^{(t)} = [\mathbf{A}^{(t)}]^{-1} \nabla L(\theta^{(t)})$$ only needs to be calculated once. Cost of line search mainly lies in objective function evaluation.

• How to approximate $-\nabla^2L(\theta)$? More of an art than science. Often requires problem specific analysis.

• Taking $\mathbf{A} = \mathbf{I}$ leads to the method of steepest ascent, aka gradient ascent.

3  Fisher's scoring method

• Fisher's scoring method: replace $- \nabla^2L(\theta)$ by the expected Fisher information matrix $$\mathbf{FIM}(\theta) = \mathbf{E}[-\nabla^2L(\theta)] = \mathbf{E}[\nabla L(\theta) \nabla L(\theta)^T] \succeq \mathbf{0}_{p \times p},$$ which is psd under exchangeability of expectation and differentiation.

  Therefore the Fisher's scoring algorithm iterates according to $$\boxed{ \theta^{(t+1)} = \theta^{(t)} + s [\mathbf{FIM}(\theta^{(t)})]^{-1} \nabla L(\theta^{(t)})}.$$

4  Generalized linear model (GLM) (KL 14.7)

4.1  Logistic regression

Let's consider a concrete example: logistic regression.

• The goal is to predict whether a credit card transaction is fraud ($y_i=1$) or not ($y_i=0$). Predictors ($\mathbf{x}_i$) include: time of transaction, last location, merchant, ...

• $y_i \in \{0,1\}$, $\mathbf{x}_i \in \mathbb{R}^{p}$. Model $y_i \sim$Bernoulli$(p_i)$.

• Logistic regression. Density $$\begin{eqnarray*} f(y_i|p_i) &=& p_i^{y_i} (1-p_i)^{1-y_i} \\ &=& e^{y_i \ln p_i + (1-y_i) \ln (1-p_i)} \\ &=& e^{y_i \ln \frac{p_i}{1-p_i} + \ln (1-p_i)}, \end{eqnarray*}$$ where $$\begin{eqnarray*} \mathbf{E} (y_i) = p_i &=& \frac{e^{\eta_i}}{1+ e^{\eta_i}} \quad \text{(mean function, inverse link function)} \\ \eta_i = \mathbf{x}_i^T \beta &=& \ln \left( \frac{p_i}{1-p_i} \right) \quad \text{(logit link function)}. \end{eqnarray*}$$

• Given data $(y_i,\mathbf{x}_i)$, $i=1,\ldots,n$,

$$\begin{eqnarray*} L_n(\beta) &=& \sum_{i=1}^n \left[ y_i \ln p_i + (1-y_i) \ln (1-p_i) \right] \\ &=& \sum_{i=1}^n \left[ y_i \mathbf{x}_i^T \beta - \ln (1 + e^{\mathbf{x}_i^T \beta}) \right] \\ \nabla L_n(\beta) &=& \sum_{i=1}^n \left( y_i \mathbf{x}_i - \frac{e^{\mathbf{x}_i^T \beta}}{1+e^{\mathbf{x}_i^T \beta}} \mathbf{x}_i \right) \\ &=& \sum_{i=1}^n (y_i - p_i) \mathbf{x}_i = \mathbf{X}^T (\mathbf{y} - \mathbf{p}) \\ - \nabla^2L_n(\beta) &=& \sum_{i=1}^n p_i(1-p_i) \mathbf{x}_i \mathbf{x}_i^T = \mathbf{X}^T \mathbf{W} \mathbf{X}, \quad \text{where } \mathbf{W} &=& \text{diag}(w_1,\ldots,w_n), w_i = p_i (1-p_i) \\ \mathbf{FIM}_n(\beta) &=& \mathbf{E} [- \nabla^2L_n(\beta)] = - \nabla^2L_n(\beta). \end{eqnarray*}$$

• Newton's method == Fisher's scoring iteration: $$\begin{eqnarray*} \beta^{(t+1)} &=& \beta^{(t)} + s[-\nabla^2 L(\beta^{(t)})]^{-1} \nabla L(\beta^{(t)}) \\ &=& \beta^{(t)} + s(\mathbf{X}^T \mathbf{W}^{(t)} \mathbf{X})^{-1} \mathbf{X}^T (\mathbf{y} - \mathbf{p}^{(t)}) \\ &=& (\mathbf{X}^T \mathbf{W}^{(t)} \mathbf{X})^{-1} \mathbf{X}^T \mathbf{W}^{(t)} \left[ \mathbf{X} \beta^{(t)} + s(\mathbf{W}^{(t)})^{-1} (\mathbf{y} - \mathbf{p}^{(t)}) \right] \\ &=& (\mathbf{X}^T \mathbf{W}^{(t)} \mathbf{X})^{-1} \mathbf{X}^T \mathbf{W}^{(t)} \mathbf{z}^{(t)}, \end{eqnarray*}$$ where $$\mathbf{z}^{(t)} = \mathbf{X} \beta^{(t)} + s(\mathbf{W}^{(t)})^{-1} (\mathbf{y} - \mathbf{p}^{(t)})$$ are the working responses. A Newton's iteration is equivalent to solving a weighed least squares problem $\sum_{i=1}^n w_i (z_i - \mathbf{x}_i^T \beta)^2$. Thus the name IRWLS (iteratively re-weighted least squares).

4.2  GLM

Let's consider the more general class of generalized linear models (GLM).

Family	Canonical Link	Variance Function
Normal	$\eta=\mu$	1
Poisson	$\eta=\log \mu$	$\mu$
Binomial	$\eta=\log \left( \frac{\mu}{1 - \mu} \right)$	$\mu (1 - \mu)$
Gamma	$\eta = \mu^{-1}$	$\mu^2$
Inverse Gaussian	$\eta = \mu^{-2}$	$\mu^3$

• $Y$ belongs to an exponential family with density $$p(y|\theta,\phi) = \exp \left\{ \frac{y\theta - b(\theta)}{a(\phi)} + c(y,\phi) \right\}.$$

  • $\theta$: natural parameter.
  • $\phi>0$: dispersion parameter.
    GLM relates the mean $\mu = \mathbf{E}(Y|\mathbf{x})$ via a strictly increasing link function $$g(\mu) = \eta = \mathbf{x}^T \beta, \quad \mu = g^{-1}(\eta)$$

• Score, Hessian, information

$$\begin{eqnarray*} \nabla L_n(\beta) &=& \sum_{i=1}^n \frac{(y_i-\mu_i) \mu_i'(\eta_i)}{\sigma_i^2} \mathbf{x}_i \\ \,- \nabla^2 L_n(\boldsymbol{\beta}) &=& \sum_{i=1}^n \frac{[\mu_i'(\eta_i)]^2}{\sigma_i^2} \mathbf{x}_i \mathbf{x}_i^T - \sum_{i=1}^n \frac{(y_i - \mu_i) \mu_i''(\eta_i)}{\sigma_i^2} \mathbf{x}_i \mathbf{x}_i^T \\ & & + \sum_{i=1}^n \frac{(y_i - \mu_i) [\mu_i'(\eta_i)]^2 (d \sigma_i^{2} / d\mu_i)}{\sigma_i^4} \mathbf{x}_i \mathbf{x}_i^T \\ \mathbf{FIM}_n(\beta) &=& \mathbf{E} [- \nabla^2 L_n(\beta)] = \sum_{i=1}^n \frac{[\mu_i'(\eta_i)]^2}{\sigma_i^2} \mathbf{x}_i \mathbf{x}_i^T = \mathbf{X}^T \mathbf{W} \mathbf{X}. \end{eqnarray*}$$

• Fisher scoring method $$\beta^{(t+1)} = \beta^{(t)} + s [\mathbf{FIM}(\beta^{(t)})]^{-1} \nabla L_n(\beta^{(t)})$$ IRWLS with weights $w_i = [\mu_i(\eta_i)]^2/\sigma_i^2$ and some working responses $z_i$.

• For canonical link, $\theta = \eta$, the second term of Hessian vanishes and Hessian coincides with Fisher information matrix. Convex problem 😄 $$\text{Fisher's scoring == Newton's method}.$$

• Non-canonical link, non-convex problem 😞 $$\text{Fisher's scoring algorithm} \ne \text{Newton's method}.$$ Example: Probit regression (binary response with probit link). $$\begin{eqnarray*} y_i &\sim& \text{Bernoulli}(p_i) \\ p_i &=& \Phi(\mathbf{x}_i^T \beta) \\ \eta_i &=& \mathbf{x}_i^T \beta = \Phi^{-1}(p_i). \end{eqnarray*}$$ where $\Phi(\cdot)$ is the cdf of a standard normal.

• Julia, R and Matlab implement the Fisher scoring method, aka IRWLS, for GLMs.

  • GLM.jl package.

5  Nonlinear regression - Gauss-Newton method (KL 14.4-14.6)

• Now we finally get to the problem Gauss faced in 1800!
  Relocate Ceres by fitting 41 observations to a 6-parameter (nonlinear) orbit.

• Nonlinear least squares (curve fitting): $$\text{minimize} \,\, f(\beta) = \frac{1}{2} \sum_{i=1}^n [y_i - \mu_i(\mathbf{x}_i, \beta)]^2$$ For example, $y_i =$ dry weight of onion and $x_i=$ growth time, and we want to fit a 3-parameter growth curve $$\mu(x, \beta_1,\beta_2,\beta_3) = \frac{\beta_3}{1 + e^{-\beta_1 - \beta_2 x}}.$$

• "Score" and "information matrices" $$\begin{eqnarray*} \nabla f(\beta) &=& - \sum_{i=1}^n [y_i - \mu_i(\beta)] \nabla \mu_i(\beta) \\ \nabla^2 f(\beta) &=& \sum_{i=1}^n \nabla \mu_i(\beta) \nabla \mu_i(\beta)^T - \sum_{i=1}^n [y_i - \mu_i(\beta)] \nabla^2 \mu_i(\beta) \\ \mathbf{FIM}(\beta) &=& \sum_{i=1}^n \nabla \mu_i(\beta) \nabla \mu_i(\beta)^T = \mathbf{J}(\beta)^T \mathbf{J}(\beta), \end{eqnarray*}$$ where $\mathbf{J}(\beta)^T = [\nabla \mu_1(\beta), \ldots, \nabla \mu_n(\beta)] \in \mathbb{R}^{p \times n}$.

• Gauss-Newton (= "Fisher's scoring algorithm") uses $\mathbf{I}(\beta)$, which is always psd. $$\boxed{ \beta^{(t+1)} = \beta^{(t)} + s [\mathbf{FIM} (\beta^{(t)})]^{-1} \nabla L(\beta^{(t)}) }$$

• Levenberg-Marquardt method, aka damped least squares algorithm (DLS), adds a ridge term to the approximate Hessian $$\boxed{ \beta^{(t+1)} = \beta^{(t)} + s [\mathbf{FIM} (\beta^{(t)}) + \tau \mathbf{I}_p]^{-1} \nabla L(\beta^{(t)}) }$$ bridging between Gauss-Newton and steepest descent.

• Other approximation to Hessians: nonlinear GLMs.
  See KL 14.4 for examples.