Table of Contents¶
Computer Arithmetics¶
versioninfo()
Units of computer storage¶
bit=binary+digit(coined by statistician John Tukey).byte= 8 bits.- KB = kilobyte = $10^3$ bytes.
- MB = megabytes = $10^6$ bytes.
- GB = gigabytes = $10^9$ bytes. Typical RAM size.
- TB = terabytes = $10^{12}$ bytes. Typical hard drive size. Size of NYSE each trading session.
- PB = petabytes = $10^{15}$ bytes.
- EB = exabytes = $10^{18}$ bytes. Size of all healthcare data in 2011 is ~150 EB.
- ZB = zetabytes = $10^{21}$ bytes.
Julia function Base.summarysize shows the amount of memory (in bytes) used by an object.
x = rand(100, 100)
Base.summarysize(x)
varinfo() function prints all variables in workspace and their sizes.
varinfo() # similar to Matlab whos()
Storage of Characters¶
- Plain text files are stored in the form of characters:
.jl,.r,.c,.cpp,.ipynb,.html,.tex, ... - ASCII (American Code for Information Interchange): 7 bits, only $2^7=128$ characters.
# integers 0, 1, ..., 127 and corresponding ascii character
[0:127 Char.(0:127)]
- Extended ASCII: 8 bits, $2^8=256$ characters.
# integers 128, 129, ..., 255 and corresponding extended ascii character
# show(STDOUT, "text/plain", [128:255 Char.(128:255)])
[128:255 Char.(128:255)]
Unicode: UTF-8, UTF-16 and UTF-32 support many more characters including foreign characters; last 7 digits conform to ASCII.
UTF-8 is the current dominant character encoding on internet.
- Julia supports the full range of UTF-8 characters. You can type many Unicode math symbols by typing the backslashed LaTeX symbol name followed by tab.
# \beta-<tab>
β = 0.0
# \beta-<tab>-\hat-<tab>
β̂ = 0.0
- For a table of unicode symbols that can be entered via tab completion of LaTeX-like abbreviations: https://docs.julialang.org/en/v1.1/manual/unicode-input/#Unicode-Input-1
Integers: fixed-point number system¶
Fixed-point number system is a computer model for integers $\mathbb{Z}$.
The number of bits and method of representing negative numbers vary from system to system.
- The
integertype in R has $M=32$ or 64 bits, determined by machine word size. - Matlab has
(u)int8,(u)int16,(u)int32,(u)int64.
- The
Julia has even more integer types. Using Tom Breloff's
Plots.jlandGraphRecipes.jlpackages, we can visualize the type tree underInteger- Storage for a
SignedorUnsignedinteger can be $M = 8, 16, 32, 64$ or 128 bits. - GraphRecipes.jl package has a convenience function for plotting the type hiearchy.
- Storage for a
using GraphRecipes, Plots
#pyplot(size=(800, 600))
gr(size=(600, 400))
theme(:default)
plot(Integer, method=:tree, fontsize=4)
Signed integers¶
First bit indicates sign.
0for nonnegative numbers1for negative numbers
Two's complement representation for negative numbers.
- Sign bit is set to 1
- remaining bits are set to opposite values
- 1 is added to the result
- Two's complement representation of a negative integer
xis same as the unsigned integer2^64 + x.
@show typeof(18)
@show bitstring(18)
@show bitstring(-18)
@show bitstring(UInt64(Int128(2)^64 - 18)) == bitstring(-18)
@show bitstring(2 * 18) # shift bits of 18
@show bitstring(2 * -18); # shift bits of -18
- Two's complement representation respects modular arithmetic nicely.
Addition of any two signed integers are just bitwise addition, possibly modulo $2^M$

Arithmetics (addition, substraction, multiplication) of integers are exact except for the possiblity of overflow and underflow.
Range of representable integers by $M$-bit signed integer is $[-2^{M-1},2^{M-1}-1]$.
- Julia functions
typemin(T)andtypemax(T)give the lowest and highest representable number of a typeTrespectively
- Julia functions
typemin(Int64), typemax(Int64)
for T in [Int8, Int16, Int32, Int64, Int128]
println(T, '\t', typemin(T), '\t', typemax(T))
end
Unsigned integers¶
- For unsigned integers, the range is $[0,2^M-1]$.
for t in [UInt8, UInt16, UInt32, UInt64, UInt128]
println(t, '\t', typemin(t), '\t', typemax(t))
end
BigInt¶
Julia BigInt type is arbitrary precision.
@show typemax(Int128)
@show typemax(Int128) + 1 # modular arithmetic!
@show BigInt(typemax(Int128)) + 1;
Overflow and underflow for integer arithmetic¶
R reports NA for integer overflow and underflow.
Julia outputs the result according to modular arithmetic.
@show typemax(Int32)
@show typemax(Int32) + Int32(1); # modular arithmetics!
using RCall
R"""
.Machine$integer.max
"""
R"""
M <- 32
big <- 2^(M-1) - 1
as.integer(big)
"""
R"""
as.integer(big+1)
"""
Real numbers: floating-number system¶
Floating-point number system is a computer model for real numbers.
Most computer systems adopt the IEEE 754 standard, established in 1985, for floating-point arithmetics.
For the history, see an interview with William Kahan.In the scientific notation, a real number is represented as $$\pm d_0.d_1d_2 \cdots d_p \times b^e.$$ In computer, the base is $b=2$ and the digits $d_i$ are 0 or 1.
Normalized vs denormalized numbers. For example, decimal number 18 is $$ +1.0010 \times 2^4 \quad (\text{normalized})$$ or, equivalently, $$ +0.1001 \times 2^5 \quad (\text{denormalized}).$$
In the floating-number system, computer stores
- sign bit
- the fraction (or mantissa, or significand) of the normalized representation
- the actual exponent plus a bias
using GraphRecipes, Plots
#pyplot(size=(800, 600))
gr(size=(600, 400))
theme(:default)
plot(AbstractFloat, method=:tree, fontsize=4)
Double precision (Float64)¶

Double precision (64 bits = 8 bytes) numbers are the dominant data type in scientific computing.
In Julia,
Float64is the type for double precision numbers.First bit is sign bit.
$p=52$ significant bits.
11 exponent bits: $e_{\max}=1023$, $e_{\min}=-1022$, bias=1023.
$e_{\text{min}}-1$ and $e_{\text{max}}+1$ are reserved for special numbers.
range of magnitude: $10^{\pm 308}$ in decimal because $\log_{10} (2^{1023}) \approx 308$.
precision to the $- \log_{10}(2^{-52}) \approx 15$ decimal point.
println("Double precision:")
@show bitstring(Float64(18)) # 18 in double precision
@show bitstring(Float64(-18)); # -18 in double precision
Single precision (Float32)¶

In Julia,
Float32is the type for single precision numbers.First bit is sign bit.
$p=23$ significant bits.
8 exponent bits: $e_{\max}=127$, $e_{\min}=-126$, bias=127.
$e_{\text{min}}-1$ and $e_{\text{max}}+1$ are reserved for special numbers.
range of magnitude: $10^{\pm 38}$ in decimal because $\log_{10} (2^{127}) \approx 38$.
precision: $- \log_{10}(2^{-23}) \approx 7$ decimal point.
println("Single precision:")
@show bitstring(Float32(18.0)) # 18 in single precision
@show bitstring(Float32(-18.0)); # -18 in single precision
Half precision (Float16)¶
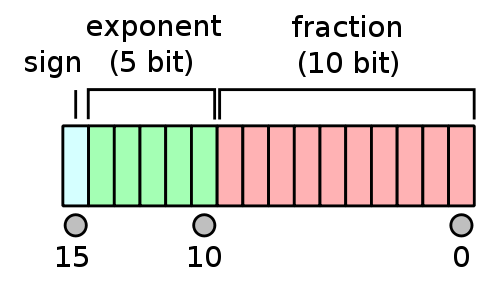
In Julia,
Float16is the type for half precision numbers.First bit is sign bit.
$p=10$ significant bits.
5 exponent bits: $e_{\max}=15$, $e_{\min}=-14$, bias=15.
$e_{\text{min}}-1$ and $e_{\text{max}}+1$ are reserved for special numbers.
range of magnitude: $10^{\pm 4}$ in decimal because $\log_{10} (2^{15}) \approx 4$.
precision: $\log_{10}(2^{10}) \approx 3$ decimal point.
println("Half precision:")
@show bitstring(Float16(18)) # 18 in half precision
@show bitstring(Float16(-18)); # -18 in half precision
Special floating-point numbers.¶
- Exponent $e_{\max}+1$ plus a zero mantissa means $\pm \infty$.
@show bitstring(Inf) # Inf in double precision
@show bitstring(-Inf); # -Inf in double precision
Exponent $e_{\max}+1$ plus a nonzero mantissa means
NaN.NaNcould be produced from0 / 0,0 * Inf, ...In general
NaN ≠ NaNbitwise. Test whether a number isNaNbyisnanfunction.
@show bitstring(0 / 0) # NaN
@show bitstring(0 * Inf); # NaN
- Exponent $e_{\min}-1$ with a zero mantissa represents the real number 0.
@show bitstring(0.0); # 0 in double precision
- Exponent $e_{\min}-1$ with a nonzero mantissa are for numbers less than $b^{e_{\min}}$.
Numbers are denormalized in the range $(0,b^{e_{\min}})$ -- graceful underflow.
@show nextfloat(0.0) # next representable number
@show bitstring(nextfloat(0.0)); # denormalized
Rounding¶
- Rounding is necessary whenever a number has more than $p$ significand bits. Most computer systems use the default IEEE 754 round to nearest mode (also called ties to even mode). Julia offers several rounding modes, the default being
RoundNearest. For example, the number 0.1 in decimal system cannot be represented accurately as a floating point number: $$ 0.1 = 1.10011001... \times 2^{-4} $$
# half precision Float16, ...110(011...) rounds down to 110
@show bitstring(Float16(0.1))
# single precision Float32, ...100(110...) rounds up to 101
@show bitstring(0.1f0)
# double precision Float64, ...001(100..) rounds up to 010
@show bitstring(0.1);
For a number with mantissa ending with ...001(100..., all 0 digits after), it's a tie and will be rounded to ...010 to make the mantissa even.
Summary¶
Single precision: range $\pm 10^{\pm 38}$ with precision up to 7 decimal digits.
Double precision: range $\pm 10^{\pm 308}$ with precision up to 16 decimal digits.
The floating-point numbers do not occur uniformly over the real number line
 Each magnitude has same number of representible numbers
Each magnitude has same number of representible numbersMachine epsilons are the spacings of numbers around 1: $$\epsilon_{\min}=b^{-p}, \quad \epsilon_{\max} = b^{1-p}.$$

@show eps(Float32) # machine epsilon for a floating point type
@show eps(Float64) # same as eps()
# eps(x) is the spacing after x
@show eps(100.0)
@show eps(0.0) # grace underflow
# nextfloat(x) and prevfloat(x) give the neighbors of x
@show x = 1.25f0
@show prevfloat(x), x, nextfloat(x)
@show bitstring(prevfloat(x)), bitstring(x), bitstring(nextfloat(x));
- In R, the variable
.Machinecontains numerical characteristics of the machine.
R"""
.Machine
"""
- Julia provides
Float16(half precision),Float32(single precision),Float64(double precision), andBigFloat(arbitrary precision).
Overflow and underflow of floating-point number¶
For double precision, the range is $\pm 10^{\pm 308}$. In most situations, underflow (magnitude of result is less than $10^{-308}$) is preferred over overflow (magnitude of result is larger than $10^{-308}$). Overflow produces $\pm \inf$. Underflow yields zeros or denormalized numbers.
E.g., the logit link function is $$p = \frac{\exp (x^T \beta)}{1 + \exp (x^T \beta)} = \frac{1}{1+\exp(- x^T \beta)}.$$ The former expression can easily lead to
Inf / Inf = NaN, while the latter expression leads to graceful underflow.floatminandfloatmaxfunctions gives largest and smallest finite number represented by a type.
for T in [Float16, Float32, Float64]
println(T, '\t', floatmin(T), '\t', floatmax(T), '\t', typemin(T),
'\t', typemax(T), '\t', eps(T))
end
Arbitrary precision¶
BigFloatin Julia offers arbitrary precision.
@show precision(BigFloat)
@show floatmin(BigFloat)
@show floatmax(BigFloat);
@show BigFloat(π); # default precision for BigFloat is 256 bits
# set precision to 1024 bits
setprecision(BigFloat, 1024) do
@show BigFloat(π)
end;
Catastrophic cancellation¶
- Scenario 1: Addition or subtraction of two numbers of widely different magnitudes: $a+b$ or $a-b$ where $a \gg b$ or $a \ll b$. We loose the precision in the number of smaller magnitude. Consider $$\begin{eqnarray*} a &=& x.xxx ... \times 2^{30} \\ b &=& y.yyy... \times 2^{-30} \end{eqnarray*}$$ What happens when computer calculates $a+b$? We get $a+b=a$!
@show a = 2.0^30
@show b = 2.0^-30
@show a + b == a
- Scenario 2: Subtraction of two nearly equal numbers eliminates significant digits. $a-b$ where $a \approx b$. Consider $$\begin{eqnarray*} a &=& x.xxxxxxxxxx1ssss \\ b &=& x.xxxxxxxxxx0tttt \end{eqnarray*}$$ The result is $1.vvvvu...u$ where $u$ are unassigned digits.
a = 1.2345678f0 # rounding
@show bitstring(a) # rounding
b = 1.2345677f0
@show bitstring(b)
@show a - b # correct result should be 1e-7
- Implications for numerical computation
- Rule 1: add small numbers together before adding larger ones
- Rule 2: add numbers of like magnitude together (paring). When all numbers are of same sign and similar magnitude, add in pairs so each stage the summands are of similar magnitude
- Rule 3: avoid substraction of two numbers that are nearly equal
Algebraic laws¶
Floating-point numbers may violate many algebraic laws we are familiar with, such associative and distributive laws. See Homework 1 problems.
Further reading¶
Textbook treatment, e.g., Chapter II.2 of Computational Statistics by James Gentle (2010).
What every computer scientist should know about floating-point arithmetic by David Goldberg (1991).